▷ 삼각 함수 ◁
삼각함수는 각에 대한 함수로서 삼각형의 각과 변의 길이를 연관시킨 것.
삼각함수는 직각삼각형의 변의 길이의 비로 정의되기도 하고,
좌표평면 위의 원에서 얻어지는 다양한 선분의 길이로 정의 되기도 한다.
기본적인 삼각함수는 사인함수, 코사인함수, 탄젠트함수 가 있다.
1. 직각 삼각형 에서의 삼각 함수
출처가 밝혀지지 않은 이미지는 네이버 지식백과 에서 참조 하였습니다.
 |
시작하기전 빗변 대변 이웃변에 대한 정의를 알아두고자 기입해 둔다. 빗변 : 대각선으로 가장 긴 변 이다. 대변 : 높이에 관한 변 이다. 이웃변(아랫변/인접변) : 밑 변 이다. (빗변 대변이 아닌 변) 이미지 출처 : http://urin79.com/blog/1302016 |
 |
왼쪽의 그림과 같이 각C 가 직각인 삼각형에서 각A , 각B, 각C 와 마주보는 변의 길이를 a, b, c 라고 할때, |
 |
각A 에 대한 사인(sine), 코사인(cosine), 탄젠트(tangent) 는 왼쪽과 같이 정의 한다. |
 이미지 출처 : https://gordonoliver.tistory.com/entry/sin-cos-tan-%ED%91%9C-%ED%8A%B9%EC%88%98%EA%B0%81%EC%9D%98-%EC%82%BC%EA%B0%81%EB%B9%84-%ED%91%9C 사인, 코사인, 탄젠트를 좀더 쉽게 이해하기 위하여 이미지를 참조한다. 삼각형을 위의 그림처럼 놓았을경우 영어의 필기체를 대입하여 필기체 시작부분이 분모, 끝이 분자 로 볼 수 있다. sin 은 빗변(대각) 부터 시작하여 대변(높이)에서 끝나므로 높이/빗변 cos 은 빗변(대각) 부터 시작하여 밑변(아래)에서 끝나므로 밑변/빗변 tan 은 밑변(아래) 부터 시작하여 대변(높이)에서 끝나므로 높이/밑변 |
 |
위 세 함수의 역수를 각각 각A 에 대한 코시컨트(cosecant), 시컨트(secant), 코탄젠트(cotangent) 라 하며 왼쪽과 같이 나타 낼 수 있다. |
 |
마지막으로 세 각의 크기가 45도,45도,90도 인 직각 삼각형은 이등변삼각형 이며, 세 각의 크기가 각각 30도,60도,90도 인 직각 삼각형의 빗변의 길이는 가장 짧은 변의 길이의 두배 라는 기하학적 사실과 피타고라스 정리를 이용하면 왼쪽과 같은 결과를 얻게 된다. |
2. 일반각에 대한 삼각함수
직각 삼각형의 각은 0도 와 90도의 사이에 있으므로 위의 직각 삼각형에 대한 삼각함수는 음의각(90도보다작은각)이나
양의각(90도보다큰각)에 대해서는 적용이 되지 않는다.
삼각함수를 일반각으로 확장하기 위해서는 좌표평면 위의 한 원을 살펴보는 것이 편리하다.

x,y 좌표평면에서 원점 O을 중심으로 하고 반지름의 길이가 r 인 원을 참고하여 보자.
(좌측 이미지 참고)
그림과 같이 이 원 위의 점 P(x,y)에 대해
동경(OP)가 x축과 이루는 각의 크기를 세타(θ)라고 하면
위의 여섯 개의 삼각함수는 다음과 같이 정의 된다.
(일반각에 대한 삼각함수 정의 예시 참조)

3. 삼각항등식 ( trigonometric identitiy )
삼각항등식은 삼각함수에 관한 방정식으로서 양변이 모든 각에 대해 항상 성립하는 항등식을 의미한다.
이 외의 자세한 사항은 네이버 지식 백과를 참조하도록한다.
오늘은 기본적인 개념에대하여 정리하고 공부하도록 하기위함 이기 때문에 좀더 상세한 공식은 생략한다.
https://terms.naver.com/entry.naver?docId=3340633&cid=60207&categoryId=60207
삼각함수
삼각함수는 각에 대한 함수로서 삼각형의 각과 변의 길이를 연관시킨 것이다. 삼각함수는 삼각형의 연구뿐만 아니라 소리나 빛의 파동과 같은 다양한 주기적 현상을 설명하는 데 이용된다. 삼
terms.naver.com
▷ 삼각비 ◁
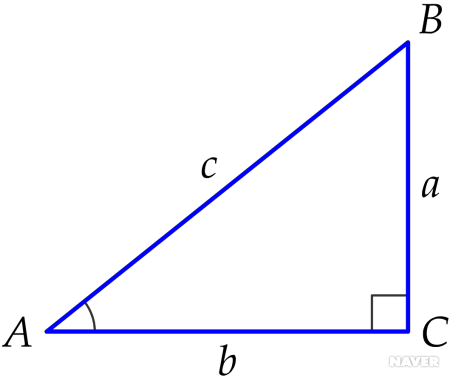
삼각비란 직각삼각형 ABC에서의 '두 변의 길이의 비' 를 의미 한다.
직각삼각형 ABC에서 각 C가 직각일때
sin A, cos A, tan A 를 합쳐서 '삼각비' 라고 한다.
(참고. 삼각비는 도형의 넓이와는 상관이 없으며 닮은 도형에서 삼각비는 일정함)
<< ( 1. 직각 삼각형 에서의 삼각 함수 ) 의 이미지를 다시한번 참고하자.
특수각의 삼각비 (공식 표)
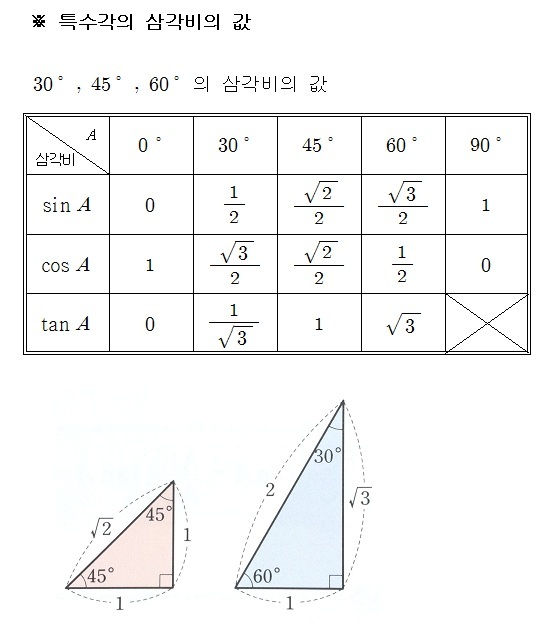
삼각비 특수각 공식 (표) 구하는 방법
정사각형이나 정삼각형을 반으로 잘라서 특수한 직각삼각형을 만들 수 있는데요. 그렇게 만들어진 직각삼각형으로 부터 삼각비 특수각을 알아내고 외워야 합니다. 먼저, 정사각형에 대각선을
coderlife.tistory.com
삼각비에대하여 간결하게 정리해놓은 블로그를 참조 하도록 하자.
'공부' 카테고리의 다른 글
| C++ 디자인패턴 - 싱글톤(싱글턴) (0) | 2022.12.12 |
|---|---|
| 비트연산자 & 쉬프트연산자 (0) | 2022.12.12 |
| Win32 API 프로시저 / 메시지 / 메시지 루프 / 메시지 큐 (0) | 2022.12.03 |
| C++ 메모리영역 복습 (1) | 2022.12.01 |
| C++ static & const 복습 (0) | 2022.12.01 |


댓글