이진탐색트리?
이진 방식의 탐색을 하기 위한 구조 입니다.
이진탐색트리에서 모든 노드는 아래의 규칙을 가지고 있습니다.
- 모든 노드의 key는 중복이 되지않습니다.
- 왼쪽방향의 자식 노드는 부모값보다 작다.
- 오른쪽방향의 자식 노드는 부모값보다 크다.
각각의 노드들이 중앙 요소가 되며 임의의 어떤 노드의 왼쪽 서브트리에는 해당 노드보다 작은 값들만,
반대로 어떤 노드의 오른쪽 서브트리에는 해당 노드보다 큰 값들만 있습니다.
이진탐색트리의 특징
장점?
1. 일반 적으로 이진 탐색의 중앙 요소를 알아야 왼쪽과 오른쪽 두곳의 트리를 나눌 수 있기 때문에
"배열"에서만 사용할 수 있습니다.
즉, 배열구조가아닌 연결리스트 혹은 동적으로 크기가 변하는 배열은 사용할 수 없습니다!
2. 배열을 사용하여 탐색할 때 보다 시간 복잡도가 들어듭니다.[배열: O(1),이진탐색트리:O(logN)]
3. 동적으로 데이터 집합 크기가 바뀌고 순서가 바뀌어도 문제가 없습니다.
단점?
1. 트리 모양이 한쪽으로 치우쳐지게 된다면 위에서 언급한 시간복잡도[O(logN)]가 마치 배열을 순차탐색 하는 O(N)처럼 될 수 있습니다. 이런경우 이진탐색 트리를 이용하는 메리트는 적어집니다. [아래이미지 참조]

따라서 이진 탐색 트리에 데이터를 "추가, 삭제" 할 때 트리 모양이 한쪽으로 치우쳐지지 않고 균형있는 모양을 유지시킨다면 O(logN) → O(N) 에 가깝게 되는 것을 방지 할 수 있습니다.
*참조 : 트리의 균형을 보장하는 "레드 블랙 트리"
이진 탐색 트리의 연산 예제
// Node 클래스
class Node
{
public:
int date;
Node* leftChild = NULL; // 좌측 자식노드
Node* rightChild = NULL; // 우측 자식노드
Node(int _data, Node* _leftChild, Node* _rightChild)
:data(_data), leftChild(_leftChild), rightChild(_rightChild)
{}
};탐색
루트 노드부터 시작하여 찾을 값과 크기를 비교하며 아래 방향으로 내려오면서 찾습니다.
if (찾으려는 값이 < 현재 트리의 루트 노드의 값보다 작다면)
: 왼쪽 서브트리 (해당노드보다 작은 값들이있는 곳) 으로 내려 갑니다.
else if (찾으려는 값이 > 현재 트리의 루트 노드의 값보다 크다면)
: 오른쪽 서브트리 (해당노드보다 큰 값들이있는 곳) 으로 내려 갑니다.

위의 설명의 코드예제 (일치하는 값을 찾을 때 까지 재귀 반복 합니다)
// CASE1 트리에 목표가 있을때 true 반환
bool BST_SearchNode1(Node* tree, int target)
{
if (tree == NULL) // 트리가 비어있다면 탐색실행 X
return false;
if (tree->data == target) // 트리의 데이터에 목표가 있다면
return true; // true 반환 !
else if (tree->data > target) // 트리의 데이터가 목표보다 크다면
return BST_SearchNode1(tree->leftChild, target); // 재귀
else if (tree->data < target) // 트리의 데이터가 목표보다 작다면
return BST_SearchNode1(tree->rightChild, target); // 재귀
}
// CASE2 트리에 목표가 있다면 해당 노드를 리턴
Node* BST_SearchNode2(Node* tree, int target)
{
if (tree == NULL) // 트리가 비어있다면 탐색실행 X
return false;
if (tree->data == target) // 트리의 데이터에 목표가 있다면
return tree; // true 반환 !
else if (tree->data > target) // 트리의 데이터가 목표보다 크다면
return BST_SearchNode2(tree->leftChild, target); // 재귀
else if (tree->data < target) // 트리의 데이터가 목표보다 작다면
return BST_SearchNode2(tree->rightChild, target); // 재귀
}
삽입(추가)
이진 탐색 규칙을 만족해야 하므로 새로운 노드가 삽입(추가)될 적합한 위치 또한 이진 탐색으로 찾아야 합니다. 그래서 위의 탐색 함수 코드와 유사합니다.
이진 탐색 트리에 "삽입(추가)"된다는 것은 곧 위에부터 크기를 비교함과 동시에 내려오면서 어딘가의 왼쪽 혹은 오른쪽의 자식으로 추가 되는 것입니다.
이진 탐색 트리 규칙을 만족하며 각 레벨 마다 왼쪽 혹은 오른쪽 서브트리를 선택하면서 계속탐색 하며 내려오다가 적합한 위치 없이 마지막 끝부분(Leaf 노드)에 도달하게된다면 그 곳에 추가 됩니다.
*Leaf 노드 : 나무 가지의 제일 끝에 잎이 달리듯하여 끝 노드를 Leaf 노드라 합니다.
void BST_InsertNode(Node* tree, Node* node)
{
if (node->x < tree->x) // 현재 재귀 단계에서의 트리 루트와 크기를 비교합니다 ( 서브트리의 루트 )
{
if (tree->leftChild == NULL) // 루트보다 작으며 왼쪽이 비어있을경우 (Leaf Node)
{
tree->leftChild = node; // 좌측자식트리에 노드를 넣어줍니다.
return; // 반환
}
else //그외에는 루트보다 작지만 그자리에 이미 노드가 있을경우 재귀하여 더 내려갑니다.
BST_InsertNode(tree->leftChild, node); // 재귀
}
else if (node->x > tree->x) // 위와 반대 조건이라면
{
if (tree->rightChild == NULL) // 루트보다 작으며 오른쪽이 비어있을경우 (Leaf Node)
{
tree->rightChild = node; // 우측측자식트리에 노드를 넣어줍니다.
return; // 반환
}
else //그외에는 루트보다 작지만 그자리에 이미 노드가 있을경우 재귀하여 더 내려갑니다.
BST_InsertNode(tree->rightChild, node); // 재귀
}
}tree를 루트로 하는 서브트리로 재귀호출 하면서 계속하여 내려옵니다.
호출 방향은 좌측, 우측의 서브트리로 2개 방향(이진) 입니다.
삭제(제거)
이진 탐색 트리에서 노드 삭제는 삭제하려는 노드의 자식이 몇개인가에 따라 방법이 다릅니다.
- 삭제할 노드의 서브트리가 0개(NULL)인 경우
- 삭제할 노드의 서브트리가 1개(좌|우)인 경우
- 삭제할 노드의 서브트리가 2개(좌&우)인 경우
단순히 삭제할 노드만을 제거하는 것이 아닌 삭제하고자하는 노드의 부모와 자식을 연결 해주며 삭제헤야 하기 때문에 그 정보를 가지고 있어야 합니다.
Node* BST_SerchMinNode(Node* tree)
{
if (tree == NULL)
return NULL;
if (tree->leftChild == NULL)
{
return tree;
}
else
return BST_SerchMinNode(tree->leftChild);
}
Node* BST_RemoveNode(Node* tree, Node* parent, int target)
{
// 타겟과 일치하는 노드를 삭제할 노드 입니다.
// 삭제할 노드의 위치가 되는 노드는 tree에, 삭제할 노드의 부모는 parent에 저장합니다.
// 삭제할 노드(tree)는 removeNode에 복사해 옮겨두고 나중에 이를 리턴 합니다.
// tree의 값을 새롭게 세팅하여 이제 삭제되고 새로운 노드로 대체된 것처럼 연산합니다.
if (tree == NULL) // 이미 비어있는 트리는 삭제 불가
return NULL; // NULL 반환
Node* removeNode = NULL; // 삭제할 노드를 저장할 임시 공간
// 삭제할 노드 탐색을 시작합니다
if (tree->data > target) // 트리의 데이터가 타겟보다 크다면
removeNode = BST_RemoveNode(tree->leftChild, tree, target); //재귀
else if (tree->data < target) // 트리의 데이터가 타겟보다 작다면
removeNode = BST_RemoveNode(tree->rightChild, tree, target); // 재귀
else if (tree->data == target) // 삭제할 노드를 찾았다면
{
removeNode = tree; // 삭제된 노드 리턴할 것이기 때문에 삭제 작업전 캐싱
// 1. 삭제하려는 노드의 자식 서브트리가 0개 일때 (Leaf 노드일때)
if (tree->leftChild == NULL && tree->rightChild == NULL)
{
if (parent->leftChild == tree) // 삭제할것이 부모의 좌측과 같다면
parent->leftChild = NULL; // 무보의 좌측서브트리는 NULL
if (parent->rightChild == tree) // 부모의 우측과 같다면
parent->rightChild = NULL; // 무보의 우측서브트리는 NULL
}
// 2. 삭제하려는 노드의 자식 서브트리가 좌측혹은 우측중 1개 일때
else if (tree->leftChild == NULL || tree->rightChild == NULL)
{
Node* temp = NULL; // 임시변수 생성
if (tree->leftChild != NULL) // 왼쪽서브트리가 NULL이 아니라면(있다면)
temp = tree->leftChild;
else // 오른쪽서브트리가 NULL이 아니라면(있다면)
temp = tree->rightChild;
if (parent->leftChild == tree) // 부모의 왼쪽서브트리가 트리와같다면
parent->leftChild = temp; //부모의 왼쪽서브트리에 임시변수넣기
else
parent->rightChild = temp; //부모의 왼쪽서브트리에 임시변수넣기
}
// 3. 삭제하려는 노드의 자식 서브트리가 2개(양쪽다) 일때
else if (tree->leftChild != NULL && tree->rightChild != NULL)
{
Node* minNode_of_BiggerNodes = BST_SerchMinNode(tree->rightChild);
minNode_of_BiggerNodes = BST_RemoveNode(tree, NULL, minNode_of_BiggerNodes->data);
tree->data = minNode_of_BiggerNodes->data;
}
}
return removeNode;
}제일먼저 삭제하고자하는 타겟(노드)를 찾아야 합니다.
target과 일치하는 data를 가지고 있는 노드를 찾는 작업을 합니다.그작업을 하는 코드는 아래의 구간 입니다.
// 생략
Node* BST_RemoveNode(Node* tree, Node* parent, int target)
{
// 타겟과 일치하는 노드를 삭제할 노드 입니다.
// 삭제할 노드의 위치가 되는 노드는 tree에, 삭제할 노드의 부모는 parent에 저장합니다.
// 삭제할 노드(tree)는 removeNode에 복사해 옮겨두고 나중에 이를 리턴 합니다.
// tree의 값을 새롭게 세팅하여 이제 삭제되고 새로운 노드로 대체된 것처럼 연산합니다.
if (tree == NULL) // 이미 비어있는 트리는 삭제 불가
return NULL; // NULL 반환
Node* removeNode = NULL; // 삭제할 노드를 저장할 임시 공간
// 삭제할 노드 탐색을 시작합니다
if (tree->data > target) // 트리의 데이터가 타겟보다 크다면
removeNode = BST_RemoveNode(tree->leftChild, tree, target); //재귀
else if (tree->data < target) // 트리의 데이터가 타겟보다 작다면
removeNode = BST_RemoveNode(tree->rightChild, tree, target); // 재귀
else if (tree->data == target) // 삭제할 노드를 찾았다면
{
removeNode = tree; // 삭제된 노드 리턴할 것이기 때문에 삭제 작업전 캐싱
// 생략Node* BST_RemoveNode(Node* tree, Node* parent, int target)
항상 parent는 tree의 부모를 가리키도록 하는 것 입니다.
삭제할 노드의 부모와 삭제할 노드의 자식을 연결하지 않는다면 트리구조가 성립되지 않기때문에 부모 노드의 좌측 혹은 우측 서브트리를 업데이트 해주어야 하기 때문에 삭제할 노드의 부모가 누군지에 대한 정보도 항상 가지고 있어야 합니다.
루트 노트부터 target과 일치하는 노드를 찾기 위해 한단계(레벨)씩 아래방향으로 내려오면서 tree는 현재의 노드를 parent는 tree의 이전(상위)노드이자 부모가 됩니다. tree와 parent는 재귀를통하여 계속 업데이트 됩니다.
그렇게 계속하여 내려오다 삭제할 노드가 목표에 걸린다면
삭제할 노드를 리턴해주어야 할것이기 대문에 미리 removeNode = tree 를 사용하여 데이터를 옮깁니다.
이제 옮겨진 목표(제거할)는 다른곳으로 이동하고 이후의 데이터들이 업데이트 되게됩니다.
삭제할 노드의 서브트리가 없는 경우( 삭제할 노드가 Leaf 노드일 경우)
// 1. 삭제하려는 노드의 자식 서브트리가 0개 일때 (Leaf 노드일때)
if (tree->leftChild == NULL && tree->rightChild == NULL)
{
if (parent->leftChild == tree) // 삭제할것이 부모의 좌측과 같다면
parent->leftChild = NULL; // 무보의 좌측서브트리는 NULL
if (parent->rightChild == tree) // 부모의 우측과 같다면
parent->rightChild = NULL; // 무보의 우측서브트리는 NULL
}삭제할 대상인 tree의 부모인 parent의 leftChild 혹은 rightChild에 tree가 저장되어 있을 것 입니다.
이때 부모의 서브트리인 제거할목표를 NULL로 세팅한다면 연결은 끊어 집니다.
단, 무턱대고 끊어 놓은 것은 아닙니다.
윗단계에서 removeNode = tree 로 tree자체를 removeNode 라는 임시공간에 저장되어있습니다.

삭제할 노드의 서브트리가 1개인 경우( 삭제할 노드의 서브트리가 왼쪽 혹은 오른쪽만 있는 경우)
// 2. 삭제하려는 노드의 자식 서브트리가 좌측혹은 우측중 1개 일때
else if (tree->leftChild == NULL || tree->rightChild == NULL)
{
Node* temp = NULL; // 임시변수 생성
if (tree->leftChild != NULL) // 왼쪽서브트리가 NULL이 아니라면(있다면)
temp = tree->leftChild;
else // 오른쪽서브트리가 NULL이 아니라면(있다면)
temp = tree->rightChild;
if (parent->leftChild == tree) // 부모의 왼쪽서브트리가 트리와같다면
parent->leftChild = temp; //부모의 왼쪽서브트리에 임시변수넣기
else
parent->rightChild = temp; //부모의 왼쪽서브트리에 임시변수넣기
}tree가 왼쪽 자식 하나 있다면
삭제할 노드인 tree가 parent의 왼쪽 자식이라면 parent의 왼쪽 자식은 tree의 왼쪽 자식으로 세팅 -삭제할 노드인 tree가 parent의 오른쪽 자식이라면 parent의 오른쪽 자식은 tree의 왼쪽 자식으로 세팅
tree가 오른쪽 자식 하나 있다면
삭제할 노드인 tree가 parent의 왼쪽 자식이라면 parent의 왼쪽 자식은 tree의 오른쪽자식으로 세팅 -삭제할 노드인 tree가 parent의 오른쪽 자식이라면 parent의 오른쪽 자식은 tree의 오른쪽 자식으로 세팅

삭제할 노드의 서브트리가 2개인 경우( 삭제할 노드의 서브트리가 양쪽에있는 경우)
Node* BST_SerchMinNode(Node* tree)
{
if (tree == NULL)
return NULL;
if (tree->leftChild == NULL)
{
return tree;
}
else
return BST_SerchMinNode(tree->leftChild);
}삭제될 노드의 자리에는 이진 탐색 트리의 규칙을 만족할 수 있는 노드로 교체가 되어야 합니다.
즉, 삭제될 노드의 왼쪽 서브트리보다는 커야하되, 삭제될 노드의 오른쪽 서브트리보다는 작아야하는 규칙입니다.
이조건을 만족시키며 삭제될 노드의 자리에 올 수 있는 후보의 노드는
1. 삭제될 노드의 오른쪽 서브트리에서 가장 왼쪽에 위치한 노드
- 삭제될 노드의 왼쪽 서브트리 보다는 큰것이 보장 되어있습니다. (오른쪽 서브트리에 있기때문)
- 이 후보 노드가 채택 된다면 오른쪽 서브트리보다 작다는 것이 보장되어 있습니다. 삭제될 노드의 기존 오른쪽 서브트리 내에서 가장 작은 최소의 값이기 때문입니다.
2. 삭제될 노드의 왼쪽 서브트리에서 가장 오른쪽에 위치한 노드
- 삭제될 노드의 왼쪽 서브트리 보다는 크다는 것이 보장되어 있습니다 (왼쪽 서브트리중 가장큰것이기때문)
- 삭제될 노드의 오른쪽 서브트리 보다는 작다는 것이 보장되어 있습니다. (왼쪽 서브트리에 있기때문)
위의 두개 후보중 아무거나 채택되어도 괜찮습니다.
바로 위의 함수는 삭제할 노드를 1번의 조건으로 교체하겠다는 함수 입니다.
Node* BST_SerchMinNode(Node* tree)
BST_SerchMinNode(tree->rightChild); 호출시
오른쪽 서브리스트에서 가장 왼쪽에 위치한노드를 가져옵니다.
삭제할 tree 의 우측에서 가장 작은 값(가장작은값이지만 구조상 삭제할 tree 보다는 크다)
else if (tree->data == target) // 삭제할 노드를 찾았다면
{
removeNode = tree; // 삭제된 노드 리턴할 것이기 때문에 삭제 작업전 캐싱
// 1, 2 생략
// 3. 삭제하려는 노드의 자식 서브트리가 2개(양쪽다) 일때
else if (tree->leftChild != NULL && tree->rightChild != NULL)
{
Node* minNode_of_BiggerNodes = BST_SerchMinNode(tree->rightChild);
minNode_of_BiggerNodes = BST_RemoveNode(tree, NULL, minNode_of_BiggerNodes->data);
tree->data = minNode_of_BiggerNodes->data;
}
}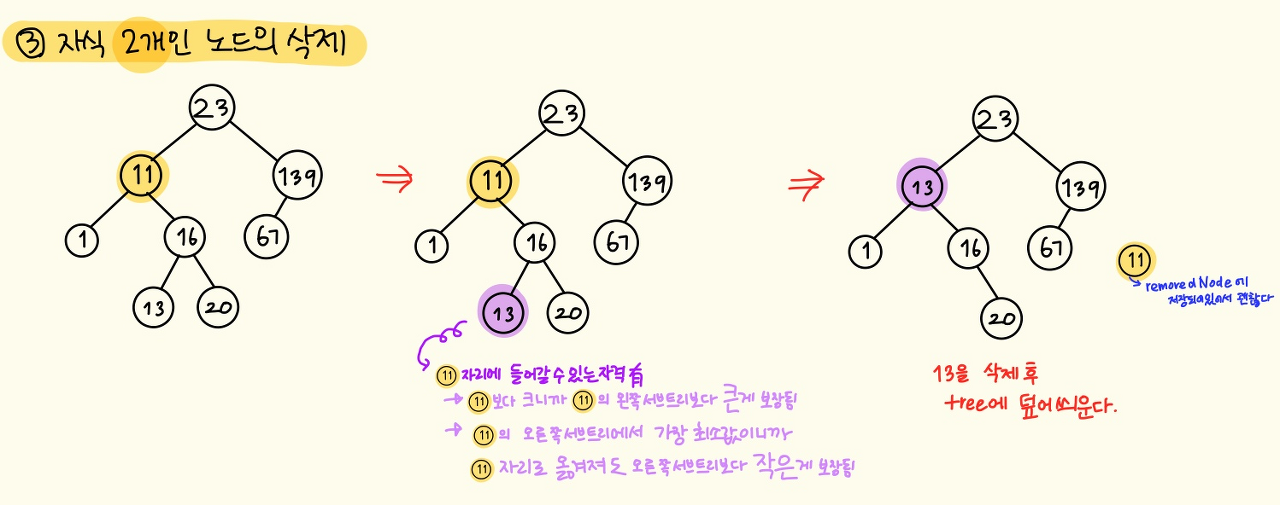
minNode_of_BiggerNode : 삭제할 노드의 tree의 오른쪽 서브트리 중 가장 최솟값 노드
minNode_of_BiggerNode 를 삭제합니다.
minNode_of_BiggerNode 또한 서브트리 몇 개를 가지고 있는 노드인지 알수 없기때문에 재귀를 이용하여
BST_RemoveNode 를 호출해서 minNode_of_BiggerNode 노드를 삭제하면 됩니다.
tree 에 minNode_of_BiggerNode 로 갱신 시켜줍니다.
tree 의 기존 왼쪽 오른쪽 서브트리는 갱신하여 data만 바꿔주면 됩니다.
* 순회 (전위 순회, 중위 순회, 후위 순회) *
https://rhksgml78.tistory.com/234
[알고리즘] 순회(전위 순회, 중위 순회, 후위 순회)
이진탐색트리의 추가 부분 입니다. [알고리즘] 이진탐색트리 이진탐색트리? 이진 방식의 탐색을 하기 위한 구조 입니다. 이진탐색트리에서 모든 노드는 아래의 규칙을 가지고 있습니다. 모든 노
rhksgml78.tistory.com
'알고리즘' 카테고리의 다른 글
| [알고리즘] A*알고리즘(Astar Algorithm) (0) | 2023.07.12 |
|---|---|
| [알고리즘] 보간 (interpolation) (0) | 2023.05.22 |
| [알고리즘] 깊이우선탐색(DFS)과 너비우선탐색(BFS) (0) | 2023.04.27 |
| [알고리즘] 빅오 표기법 (Big O notation) (0) | 2023.04.26 |
| [알고리즘/C++]하노이탑알고리즘 (1) | 2023.04.25 |




댓글