노멀 매핑(Normal Mapping)
노멀 매핑은 표면의 디테일을 높이기 위하여 사용되는 기술입니다.
일반적으로 3D 모델의 표면은 균일한 빛 반사의 특성을 가지고 있지만 실제 객체는 표면의 디테일이 있고, 함몰 및 돌출의 부분들이 존재 합니다.
노멀 매핑은 이러한 디테일을 표현하기 위하여 사용되는 기술로 3D 모델의 표면의 법선(Normal)의 벡터를 조작하여 시각적으로 디테일한 표현을 추가합니다.

공식 및 상세내용 참조 사이트
LearnOpenGL - Normal Mapping
Normal Mapping Advanced-Lighting/Normal-Mapping All of our scenes are filled with meshes, each consisting of hundreds or maybe thousands of triangles. We boosted the realism by wrapping 2D textures on these flat triangles, hiding the fact that the polygons
learnopengl.com
탄젠트 스페이스(Tangent Space)
탄젠트 스페이스는 위의 노멀 매핑을 적용하기 위하여 필요한 좌표의 공간을 의미 합니다.
각각의 픽셀의 노벌맵은 텍스처로 저장이 되는데, 이 텍스처는 주로 탄젠트 스페이스에서 표현이 됩니다.
탄젠트 스페이스는 3D 모델의 표면을 기준으로 한 로컬 좌표 공간입니다.
탄젠트 스페이스에서는 표면의 각 점에 대하여 세개의 벡터가 필요하게 됩니다.
첫번째는 법선벡터(Normal Vector)로 표면의 수직 방향을 나타 내고 있습니다.
두번째는 접선벡터(Tangent Vector)로 표면의 수평 방향을 나타 내고 있습니다.
세번째는 양질벡터(Bitangent Vector)로 법선과 접선 벡터에 수직인 벡터를 나타 내고 있습니다.
탄젠트 스페이스에서 노말맵을 적용하기 위해서는 3D 모델의 접선벡터(Tangent Vector)와 양질벡터(Bitangent Vector)를 계산해야 합니다.
이것을 위하여 모델의 각 정점에 대하여 접선벡터(Tangent Vector)와 양질벡터(Bitangent Vector)를 계산하고 이것을 통하여 접선 변환 행렬(Tangent Transform Matrix)를 생성해야 합니다.
이 행렬은 필셀 쉐이더에서 노말맵을 탄젠트스페이스 에서 월드스페이스로 변환하기 위하여 사용됩니다.
각 버텍스마다 양질벡터(B) = 법선벡터(N) * 접선벡터(T) 로 정의 됩니다. ( B = N * T)
세벡터를 축(axes)로 갖는 공간을 즉, 탄젠트스페이스(Tangent Space)입니다.
노멀맵 & 범프맵 등의 텍스처는 탄젠트 스페이스를 기준 좌표로 가지고 라이트 벡터 등은 오브젝트 스페이스를 기준으로 좌표를 가지기 때문에 같은 공간 기준 좌표로 맞춰줘야 합니다.
즉, Tangent(Local) Space <==> Object(World) Space
Object-to-Tangent Matrix =
[ Tx Ty Tz ]
[ Bx By Bz ]
[ Nx Ny Nz ]
탄젠트 스페이스(로컬)를 오브젝트 스페이스(월드)로 변환 하기 위해서는 위 행렬의 역행렬이 필요합니다.
하지만 구할 필요가 없는데 이는 하나의 회전 행렬과 같기 떄문이며 회전행렬의 역행렬은 전치행렬(Transposed Matrix) 인데 전치 행렬또한 곱해주는 순서만 바꾸어 해결이 가능하다고 합니다.
(현재 이부분이 직접 구현해보지 않았기 때문에 이해가 잘 가지 않습니다. 추가적인 이해가 필요)


결론
노멀매핑(Normal Mapping)을 구현하기 위하여 탄젠트스페이스(Tangent Space)와 연관된 계산을 수행하고 3D 모델의 표면에 디테일을 추가하여 더욱 현실적인 그래픽을 구현 할 수 있습니다.

노멀맵에 사용되는 이미지는 첨부된 이미지처럼 Blue Color 입니다.
스포이드로 측정한 기본값(Default)은 R128,G128,B255 입니다.
그림파일은 보통 0~255의 색상 값으로 이루어져 있습니다.
0(흑색) ~ 1(흰색) 밖에 값이 없으므로 - 값이 없습니다.
하지만 방향값은 - 값이 있기 때문에 - 방향을 표현하기위하여 255(1)를 반으로 나눈 128(0.5)부터 아래의 값은 -로 취급하게 됩니다.
우리가 Normal 이라고 생각하는 것은 기본값 0으로 간주합니다. 왜냐하면 평면을 바닥에 깔아둔 전제로 보기 때문입니다.
즉, 노멀맵 벡터는 0,0,1 이 기본이 됩니다.(주의, 모델마다 조금씩 다를 수 있습니다)
현재 ASSIMP에서 import 시에 노멀스페이스를 탄젠트스페이스로 사용할 것으로 정하고 있습니다.

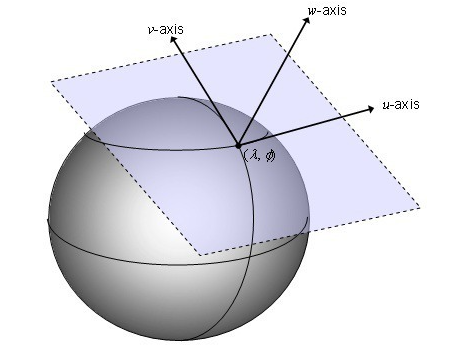
보통 평면 기준으로 나오는 법선(Normal)을 계산할 때에 한 접선을 정의 하는 것을 00스페이스 라고 하는데 법선 이라는 것은 접선면에서 수직하는 벡터를 의미합니다.
그런데 밑면의 법선과 아랫면의 법선을 동시에 저장 할 수는 없습니다.
그이유는 접선면이 달라지기 때문 입니다.
때문에 텍스처 매핑하기전 마치 세계지도처럼 평면으로 펼쳐 접선면을 통일시킨 평면도를 기준으로 노멀을 보게됩니다.
그후 돌아간 각도에따라 접선면의 각도또한 다르게되는데 이때 모델에 돌아갈 축같은 값을 정해 줍니다.
VertexType에서 normal & tangent 값을 저장하는데 normal은 원래 위를 바라보는 방향이지만 tangent는 normal 외에 밑에 깔리는 접선면의 벡터중 하나 입니다. 보통 tangent 또는 binormal 이라고 합니다.
normal은 접선면에서 수직방향의 vector 이기때문에 normal 만 저장하면 밑의 내용까지 다 알수 있는것이아닐까? 생각할수도 있습니다.
하지만 방향을 알고있다하여도 normal의 각도까지는 알 수 없습니다.
때문에 그각도를 알기위하여 추가적인방향(보통 오른쪽방향)의 벡터를 알아야 합니다.
그렇기 때문에 필요한 것이 tangent 입니다.
normal + 추가적인 수직방향의 벡터 만있다면 추가적인 다른 방향 벡터를 귀하는 것이 가능하게됩니다.
예 : UP & RIGHT 방향을안다면 FORWARD 방향을 알수있습니다.
위의 과정을 통하여 3개의 방향을 모두 갖추게 된다면 접선면에서 얼만큼 트랜스폼으로 회전되었는를 구할 수 있게 됩니다.
그렇게 하여 평면도처럼 생긴 푸른색의 노멀맵 이미지에서 컬러값을 각도에 사용 하여 빛을 받는 디퓨즈 또는 스펙큘러등에 차이를 주어 입체적인 느낌을 줄 수 있습니다.
정점에 노멀+탄젠트라는 벡터를 적용하고 노멀맵의 벡터값을 추가시키는 것으로 효과를 줍니다.
Vertex Type 을 VertexModel 으로 설정하고 쉐이더 파일을 추가 합니다.
//VertexType.h
struct VertexModel
{
VertexModel()
{
};
VertexModel(Vector3 pos, Vector2 uv, Vector3 normal,
Vector3 tangent, Vector4 indices, Vector4 weights)
{
this->position = pos;
this->uv = uv;
this->normal = normal;
this->tangent = tangent;
this->indices = indices;
this->weights = weights;
};
Vector3 position;
Vector2 uv;
Vector3 normal;
Vector3 tangent;
Vector4 indices;
Vector4 weights;
static D3D11_INPUT_ELEMENT_DESC LayoutDesc[];
};Normalmapping 이 적용된 hlsl Shader 코드
#include "Common.hlsl"
struct VertexInput
{
float4 Position : POSITION0;
float2 Uv : UV0;
float3 Normal : NORMAL0;
//노멀매핑을 위하여 추가
float3 Tangent : TANGENT0;
float4 Indices : INDICES0; //정점변환때만 쓰이는 멤버
float4 Weights : WEIGHTS0; //정점변환때만 쓰이는 멤버
};
struct PixelInput
{
float4 Position : SV_POSITION;
float3 wPosition : POSITION0;
float2 Uv : UV0;
float3 Normal : NORMAL;
//노멀매핑을 위하여 추가
float3 Tangent : TANGENT;
float3 Binormal : BINORMAL;
};
PixelInput VS(VertexInput input)
{
PixelInput output;
output.Uv = input.Uv;
output.Position = mul(input.Position, World);
output.wPosition = output.Position.xyz;
output.Position = mul(output.Position, ViewProj);
output.Normal = mul(input.Normal, (float3x3) World);
//노멀매핑을 위하여 추가 (주의) 자료형 vector3 & vector4
output.Tangent = mul(input.Tangent, (float3x3) World);
// cross() : 외적함수를 이용하면 이외의 나머지 방향벡터를 알 수 있다.
// 외적은 두벡터와 수직하고있는 벡터를 구하는 공식 이다.
// 외적할때 갖추어야할 조건 = Normal&Tangent는 서로 직교(90도)상태
output.Binormal = cross(output.Normal.xyz, output.Tangent.xyz);
return output;
}
float4 PS(PixelInput input) : SV_TARGET
{
float4 BaseColor = DiffuseMapping(input.Uv);
//world space light
float3 wlight = normalize(-float3(1, -1, 1));
//world space normal
float3 normal = NormalMapping(input.Normal, input.Tangent,
input.Binormal, input.Uv);
/*
Common.hlsl 참고
float3 NormalMapping(float3 N, float3 T, float3 B, float2 Uv)
{
//Transform.h 참고
//Vector3 GetRight() { return Vector3(RT._11, RT._12, RT._13); }
//Vector3 GetUp() { return Vector3(RT._21, RT._22, RT._23); }
//Vector3 GetForward() { return Vector3(RT._31, RT._32, RT._33); }
T = normalize(T);
B = normalize(B);
N = normalize(N);
// 3 * 3 행렬 즉, 축이 3개가 있다면 회전 행렬을 만들 수 있다.
// 참고, 4 번행렬(w)는 이동값
[flatten]
if (Ka.a)
{
// 128,128,255 (기본값) -> 0,0,1
// 0.5,0.5,1.0
float3 normal = TextureN.Sample(SamplerN, Uv).rgb;
//float3 normal = float3(0.5, 0.5, 1.0);
//세개의 법선으로 회전행렬을 만듦
float3x3 TBN = float3x3(T, B, N);
// rgb (0~1,0~1,0~1) *2
// rgb (0~2,0~2,0~2) -1
// rgb (-1~1,-1~1,-1~1)
N = normal * 2.0f - 1.0f;
//매핑한 법선을 회전시키기 normal * Matrix
N = normalize(mul(N, TBN));
}
return N; // N = 0, 0, 1 원래저장된값X 기본값으로 일부러 세팅
}
*/
float diffuse = saturate(dot(wlight, normal));
float ambient = Ka.rgb;
float3 lambert = (diffuse + ambient) * Kd.rgb * BaseColor.rgb;
float3 Reflect = reflect(normalize(float3(1, -1, 1)), normal);
float3 viewDir = normalize(ViewPos.xyz - input.wPosition);
float3 specular = pow(saturate(dot(Reflect, viewDir)), Shininess) * Ks.rgb * SpecularMapping(input.Uv);
float alpha = (BaseColor.a < Opacity) ? BaseColor.a : Opacity;
return float4(lambert + specular, alpha);
// 결과적으로 정점의 위치는 그대로 이지만 노멀의 각도가 바뀌기 때문에 빛을 받는 정도가 틀려지고 깊이값의 느낌이 생긴다.
}
노멀 매핑의 효과를 적용시켜 좀더 디테일한 느낌이 추가된 것을 볼 수 있습니다.
하지만 노멀매핑은 직접적으로 오브젝트의 정점들이 늘어나거나 폴리곤이 늘어난 것이 아니기 때문에 눈속임의 기법입니다.
필수적으로 빛(Light)이 필요해지기 때문에 너무 어둡거나 밝은 곳에서는 입체적인 효과가 보기 어렵습니다.
즉, Light 적용이 안되는 Ambient에는 효과가 없습니다.
또한 함몰 및 돌출의 직접적인 굴곡이 적용되지 않았기 때문에 다방면에서 보았을경우 어색함이 있습니다.
하지만 저사양의 조건에서 조금더 질높은 효과를 높이기위해서는 아주 좋은 기법일 수 있습니다.
좀더 상세한 전체적인 코드는 ASSIMP가 완료 되고 정리할 예정입니다.
'공부 > Graphics' 카테고리의 다른 글
| [Graphics] 포스트 이펙트(Post Effect) (0) | 2023.08.07 |
|---|---|
| [Graphics] 텍스처에 그리기 RTT(Render To Texture) (0) | 2023.08.07 |
| [Graphics] 직사(Directional), 점(Point), 스포트(Spot) 라이트 (0) | 2023.08.06 |
| [Graphics] 포워드 렌더링(Forward Rendering) & 디퍼드 렌더링(Deferred Rendering) (0) | 2023.06.27 |
| [Graphics] 그림자 매핑(Shadow Mapping) & 애트라크션(Acne) (0) | 2023.06.26 |



댓글