C++ 행렬 (단위/영/전치/역/더하기/빼기/곱하기)

● 행렬 ( Matrix )

수학에서 행렬이란 수나 기호, 수식 등을 네모의 형태로 배열한 것으로 괄호로 묶어 표시한다.

3차원 이미지를 2차원  평면에 투영하거나 사실적인 움직임을 그려내기 위해서 사용한다.

핸렬은 행(row)가 열(column)이 있는 격자모양 배열에 스칼라를 나열한 것이다.

행렬 안에 나열된 스칼라를 요소(element)라한다.

행렬 이미지

---

● 단위 행렬 ( Unit Matrix / Identity Matrix )

대각 행렬의 대각요소가 모두 1인 행렬을 의미 한다.

대각선방향의 요소가 모두 1이다.

---

● 영행렬 ( Zero Matrix / null Matrix )

모든 행렬의 요소가 0인 행렬을 의미 한다.

모든 요소가 0이다.

---

● 전치행렬 ( Transpose Matrix )

이전 수업에서도 배웠었던 행렬이다. 대각선방향의 요소는 그대로이지만 행과 열의 좌표가 서로 바뀐 것이다.

A라는 행렬에서 x.y의 좌표가 서로 같으면 그대로 (ex. [0,0][1,1][2,2][3,3]...)

그외에는 x,y의 좌표가 서로 바뀐다.(ex.[1,2]->[2,1]..... [3,4]->[4,3]...)

출처 : https://py.checkio.org

---

● 역행렬 ( Inverse Matrix )

A라는 행렬에 B라는 행렬을 곱하였을때 단위행렬(대각선의요소가모두 1인행렬) 이 나온다면,

이때 B행렬을 A의 역행렬 이라 한다. (솔찍히 아직 공식에대해서 잘 모르겠다.)

간단히 이해만하고 수업시간때 집중 하도록 하자.

아래의 예시는 간단한 2x2의 행렬에 대한 역행렬 이다.

나무위키 참조 https://namu.wiki/w/%EC%97%AD%ED%96%89%EB%A0%AC

역행렬 - 나무위키

---

● 행렬의 더하기 빼기 곱하기

행렬의 더하기

2개의 행렬의 동일한 각 행렬 요소끼리 더해준다.

행렬 A, 행렬 B 가 있다고 가정하며 두 행렬을 더한다.

행렬의 빼기

2개의 행렬의 동일한 각 행렬 요소끼리 뺀다.

행렬 A, 행렬 B 가 있다고 가정하며 두 행렬을 뺀다.

행렬의 곱하기

행렬의 곱셈은 첫번째 행렬의 행의 길이와 곱하고자 하는 두번째 행렬의 열의 길이가 같아야만 성립한다.

첫 번째 행렬의 행과 두 번째 행렬의 열을 곱해서 더해주는 값이 각각의 원소들의 결과값이며,
그렇기에 결과 값이 앞의 행렬의 행개수와 뒤 행렬의 열개수로 결정이 되어지게 된다.

출처 : https://parksh86.tistory.com/132

2 x 2 행렬의 곱셈

2 x 3 행렬의 곱셈

3 x 3 행렬의 곱셈

---

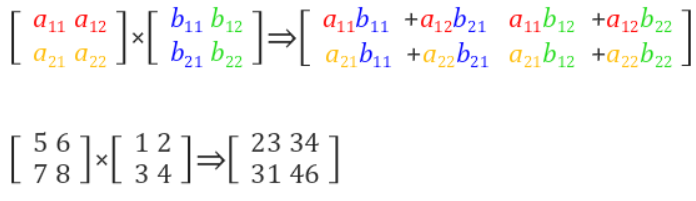
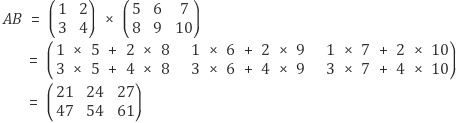
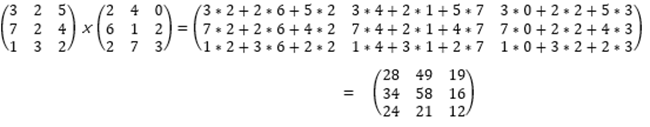
행렬의 나누기

여태까지 살펴본 것처럼 행렬은 일반적인 수와 마찬가지로 덧셈, 뺄셈, 곱셈이 가능했다.

그러나 행렬에선 어느 한 행렬이 다른 행렬은 나누는 연산은 없다.

사칙연산이라고해서 나누기까지 있을줄알고 분류해두었다! 없다고한다!

 

---

참조 사이트 

https://parksh86.tistory.com/132

[게임 수학] 행렬 - Matrix

https://steemit.com/kr-science/@chosungyun/2tgxlh

[선형대수학] 행렬 계산방법 알아보기 — Steemit